| |

|
|
|
|
Pierre
Deligne
Institute for Advanced Study
Princeton University
Visit:
May 6, 11, 13, 25, 27, June 1, 3, 8, 2004
Multizeta
Values
Thurs. May 6, 1-2 PM, IPAM 1200
Abstract: After Euler proved that 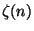 is
a rational multiple of is
a rational multiple of 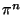 for for
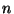 even, he wondered, as we still do, about the case
of even, he wondered, as we still do, about the case
of 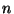 odd.
He introduced instances of what are now called multizeta values,
such as odd.
He introduced instances of what are now called multizeta values,
such as 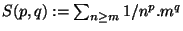 , and proved that , and proved that 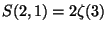 . Later, multizeta values occured in the work of Drinfeld ("associators").
They are now best understood as periods of the fundamental group
of . Later, multizeta values occured in the work of Drinfeld ("associators").
They are now best understood as periods of the fundamental group
of 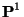 minus minus
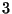 points. Together with the theory of mixed Tate
motives, this interpretation gives good upper bounds for how many
of them are linearly independant over points. Together with the theory of mixed Tate
motives, this interpretation gives good upper bounds for how many
of them are linearly independant over 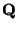 ,
and an understanding of the structure of the relations. ,
and an understanding of the structure of the relations.
All
other lectures will be held in MS 6627, 1-2 PM
Colloquium:
Through the looking glass: the case of super Riemann surfaces
Thurs. May 27, 4:00 PM, MS 6627
Abstract: As when Alice went through the looking glass, when we go over to
``super mathematics'' (introducing signs according to the Koszul
sign rule), at first nothing changes, but soon counterparts of
classical definitions or theorems take strange new forms. What
happens to the theory of Riemann surfaces will be told.
Background:
Pierre Deligne is one of the greatest mathematicians of the twentieth
century. His work has had a revolutionary impact on many fields,
including geometry, algebra, number theory, topology, and mathematical
physics. Among his achievements are his solution to the Weil conjectures
in algebraic geometry and the Ramanujan conjecture in number theory,
his solution to Hilbert's twenty-first problem and its generalization
to higher dimensions, his work on modular forms and Hodge Theory,
to mention a few.
By his own work as well as by his willingness to listen to others
and to write to them on mathematical questions he has exerted an
extraordinary influence on the mathematics and mathematicians of
his generation.
Deligne was awarded the Poincare medal of the Academy of Sciences
(Paris) in 1974, the Fields Medal in 1978, and the Crafoord prize
of the Royal Swedish Academy of Sciences in 1999. He has been a
professor at the Institute for Advanced Study at Princeton, NJ,
since 1984.
|
|
