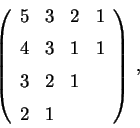UCLA Distinguished Lecturers

	Distinguished Lecture Series (DLS)
DLS Home \| Previous DLS Speakers \| People \| Seminars & Colloquia \| News \| Media Page \| UCLA Mathematics

Nikolai Reshetikhin
UC Berkeley

Thursday
November 20,
4 p.m. - 5 p.m.
MS 6227

DLS Home

Colloquium: Limit shapes of random 3D Young diagrams

An example of a plane partition of the number 26 is

29 = (5 + 3 + 2 + 1) + (4 + 3 + 1 + 1) + (3 + 2 + 1) + (2 + 1).

Its entries can be written into a quadrant in ${\mathbb{Z}}^2$ as a configuration of non-negative number non-increasing from top to bottom and from left to write:

$\begin{equation*}\left (\begin {array}{cccc} 5&3&2&1\\ \noalign{\medskip }4&3&1... ...\medskip }3&2&1\\ \noalign{\medskip }2&1\end {array} \right )\,,\end{equation*}$

(1)

A 3D Young diagram is discrete surface over a defined by the height function given by entries of a plane partition. Consider random 3D Young diagrams distributed as $q^{\vert volume\vert}$ where the volume is the total number of boxes in the diagram ( or the sum of entries of the corresponding plane partition).

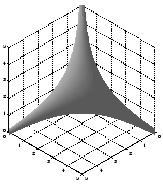
As $q\to 1$ this distribution has most probable plane partition which is called the limit shape which is sketched below.

**Figure:** The limit shape
$\scalebox{0.3}{\includegraphics{3dlimshape.eps}}$

Professor Reshetikhin will discuss this phenomenon and the microscopic fluctuations of the random plane partition near this limit shape.

If time permits he will discuss similar phenomena in other problems: in random matrices, in matching problems also known as dimer models in statistical mechanics.

For questions or comments please contact webmaster@math.ucla.edu